Turfgrass soil sampling, part 7 of 7

The summary so far is this:

• standard recommendations for turfgrass sampling are to take 12 or more cores from each area and composite them into one sample
• I’ve been taking 5 cores and compositing them
• Donohue’s research in Virginia led him to recommend taking 20 subsamples and compositing them
• The article by Lawrence et al. suggests that cores should not be composited

I’ve been wondering if my usual practice of 5 subsamples per green were enough (or too many). Last year I took 30 cores from a 1,092 m² double green in Bangkok and tested them individually. That works out to 1 sample every 36 m².

I made some calculations about the number of samples required. I’ll use the Mehlich 3 phosphorus results as an example. These are the soil test phosphorus data for those 30 cores in units of mg/kg.

31 23 29 25 25 29 24 27 26 20 19 30 29 23 24 28 21 24 32 32 22 20 33 24 23 34 24 25 24 21

I took random draws from those results, selecting 1 core, or 2, or 3, all the way up to 30 cores. And from those cores that were randomly drawn, I calculated the geometric mean, as recommended by Lawrence et al. I did that 200 times, and then plotted the means that were obtained from taking 1 up to 30 cores. This is simulating composite sampling from 1 core up to 30 cores on the same green.

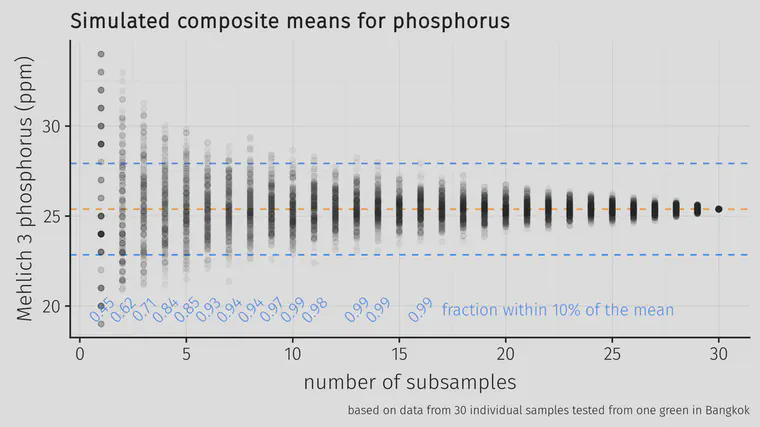
Looking at the fraction of the simulations that returned a mean within 10% of the known mean, the fraction goes above 90% (marked with a horizontal dashed line in the chart below) once there were 6 or more subsamples.

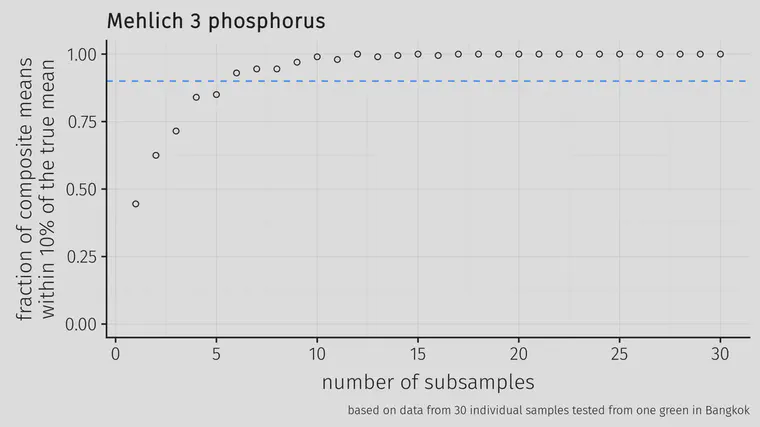
For phosphorus, once 6 cores were composited from this area, the mean soil test P was within 10% of the known mean more than 90% of the time.

I made the same calculation for other elements, and it was 6 subsamples for K, 5 for Ca, 4 for Mg, and 6 for S.

This green was 1,092 m² so 6 cores from this area would be 1 core from every 182 m². Another way to express this is 0.55 cores required per 100 m² or 0.51 samples required per 1,000 ft². That’s how many samples would be required to get a test result within 10% of the true mean of the area, 90% of the time.

The 5 subsamples I’ve been compositing per green is about twice that sampling density; if nutrient variability within the green I tested in Bangkok is similar to other greens, then I am probably getting a mean value within 10% of the true mean almost 100% of the time.

The implications of all this include:

• a few subsamples per green are probably enough to get a result close to the mean value of the green
• current recommendations for 12 or more subsamples seem to be excessive, but I need to check variability on more greens
• testing individual cores, rather than composited samples, is probably a better way to do soil testing