A number between 0 and 1: using the turfgrass growth potential

Every turf manager knows that temperature has a huge influence on the growth rate of the grass. Consequently, mowing, fertilizing, overseeding, winter dormancy, heat stress of cool season grasses, and much more are all directly influenced by temperature.

I find it especially convenient to make use of the turfgrass growth potential (GP), a number between 0 and 1 that represents the proximity of the actual temperature to the optimum temperature for growth. The turfgrass GP was developed by Wendy Gelernter and Larry Stowell at PACE Turf and their 2005 GCM article about GP is on my list of 5 articles every greenkeeper should read.

The turfgrass GP was the topic of my turfgrass talk column in the July/August 2014 issue of GCM China. In the article, I explained what GP is:

By expressing the temperature as a number between 0 and 1, we can get an idea of how much the grass has the potential to grow based on how close the actual temperature is to the optimum temperatures for growth … At frst glance it might look complicated, but it is actually quite simple. There is a minimum value of 0 if the actual temperature is very different from the optimum growth temperature. A maximum value of 1 means the actual temperature is the same as the optimum growth temperature. The GP value, then, is simply a number that says how close the actual temperature is to the optimum temperature.

Download Turf growth and temperatures in Chinese or in English.

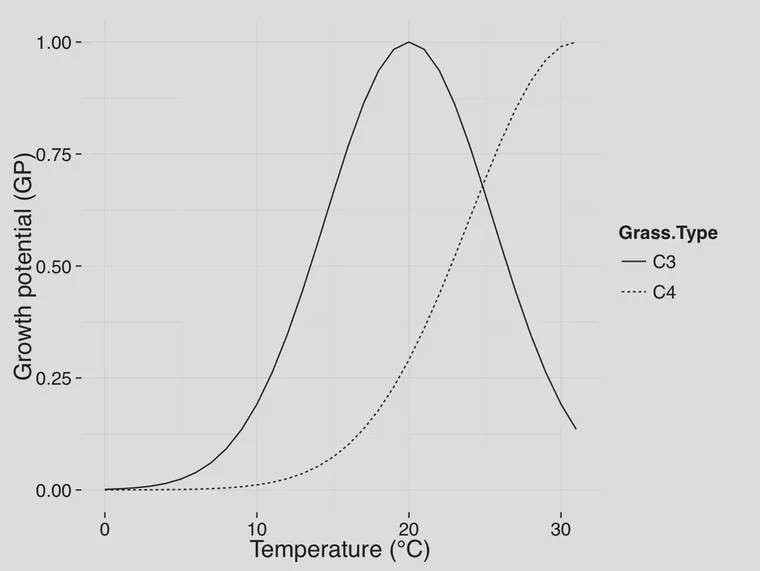
You can get the equation to calculate GP from temperature by downloading the PACE TURF climate appraisal forms, or make the calculation yourself using the growth potential equation:

$GP = e^{-0.5(\frac{t-t_o}{var})^2}$

where, $GP$ is growth potential, a value from 0 to 1; $e$ is the base of the natural logarithm, approximately 2.71828; $t$ is the actual mean temperature; $t_o$ is the optimum temperature, typically set at 20°C for C₃ grass and $\ge$ 31°C for C₄ grass; and $var$ is the variance which adjusts the shape of the curve, 5.5 for C₃ species and 7 for C₄ species when using °C.

An alternative expression of the equation generates the same result.

$GP = \frac{1}{e^{{0.5}(\frac{t-t_o}{var})^2}}$